ピークアウト　

ピークアウトしただぁ？

前回のコラムでこの度のコロナ禍の波は東京はすでにピークアウトしているとお伝えしたのですが、あちらこちらから「お前はピークアウトしていると言うが、一向に減らないじゃないか。」というお叱りを頂きました。

これはちょっと説明が必要かもしれません。

当コラムが「ピークアウト」と言う場合、それは数理社会学的な観測に基づいての見解です。その基礎にあるのは統計学です。

統計学というのは一般にある程度以上の数のバラツキのあるデータの性質を調べたり、大きなデータから一部を抜き取って、その抜き取ったデータの性質を調べて、元の大きなデータの性質を理解するための体系的な学問です。大きなデータを母集団と呼び、抜き取った一部のデータを標本と呼びます。

統計学という学問はしっかりと学んでおくととても役に立ちます。当オフィスは必ずしも統計学を専門とはしておりませんが、筆者が経済学部の講義の中で統計学の入門的講義を受講していたこと、大学院の研究室で統計学的知識がないと読めない教科書と取り組んだためにその基礎を学び直す機会があったことなどから、統計の入門的知識程度を持って数理社会学の論文と格闘している次第です。

さて、統計学の何が役に立つかといえば、事態の大まかな様相を把握できること及び近い将来の予測が立てやすいことです。

またベイズ推定という手法を用いると、将来を予測するだけでなく、観測された事実からその原因を確率的に推論することも可能となります。さらに主観的な確率を基に計算しておいて、現実の事象により改訂を繰り返して高い客観性を得ることもできます。特に現在では高速なコンピュータを用いて、事前分布の情報がまったく無い場合でも一様分布などの分布を用い、異なる事前確率分布からマルコフ連鎖モンテカルロ法などで安定した事後確率分布を得ることにより母集団を決定しにくい医学上の問題などへの応用が可能となっています。

東京のピークアウト程度の分析なら高速なコンピュータと言っても「富岳」などを持ち出す必要はなく、筆者の書斎にある事務用PCとエクセルでも簡単に計算ができます。

どういうことなのでしょうか

さて、筆者は統計の専門家ではありませんので統計学の話の細部に入るつもりはありませんが、それでは「ピークアウト」が何を意味するのかを説明します。

毎日テレビでは「感染者の増加に歯止めがかからない。」として毎日のPCR検査陽性判定者数を「感染者数」と偽って報道を続けています。

その数字が文字通り過去最大になると大喜びで「過去最多」とはしゃぎ、同列首位となると仕方ないので「過去最多に並んだ。」と表現します。

この結果、テレビでは連日「サイタ、サイタ」「ナランダ、ナランダ」とチューリップの歌の大合唱を聴かされることになります。

とにかく何かの理由をつけて不安を煽らなければならないので、テレビ局はいろいろな理屈を探し出します。「同じ曜日としては最多」とか「過去一週間で最多」とかは聞き飽きておられると存じます。

彼らは毎日の数字が棒グラフになったグラフを見て、その高さを比べるしか能がありません。その解説をしている専門家たちも同様です。

したがって、現在のように連日の陽性判定者数が右肩上がりの時にはこの先どこまで上昇していくのかが彼らには分かりません。

最近はそれでも1週間の移動平均を取って日々のデコボコを修正して見るということができるようになりましたが、いずれも過去の動きしか見ていません。

なぜピークアウトと判断したか

しかし、ちょっとでも統計学を齧った者なら、移動平均くらいで騙されることはありません。

彼らは増大する陽性判定者数の増加率を見ています。

これは連日の陽性判定者数を見るのではなく、その増え方を見るということです。前日の1.5倍になった、その前は1.2倍だったというように、増加率を見るのです。

感染症が流行すると、一般的には増加率が飛躍的に上昇していきます。増加率が一定で動かなくても、全体では凄まじい数になります。

例えば、一人から始まった感染の毎日の死者の増加率が2.0だった場合、28日目には日本人がすべて死亡し、34日目には世界中が死滅します。

統計学的観点から感染症を見る場合、この増加率が増大から縮小に転じたポイントのひとつ前の観測ポイントをピークといいます。

このため、その時点での増加率が１．０より大きい場合には依然として増加は続くのですが、増加の勢いが力を失っており、いずれ実際の数値も減少に転じます。だから、依然として増加を続けていても統計学的にはピークアウトなのです。つまり先が見えたということです。

これは重要な視点です。テレビに出てくる専門家たちはこれを理解していないのか爆発的感染に歯止めがかからないというような言い方をよくしますが、私たちが見ると明らかにピークアウトしているのにそのように不安を煽ることがよくあります。

典型的だったのは昨年の最初の緊急事態宣言でした。あれはピークアウトが完全に確認されてから発令されたので、宣言と同時に陽性判定者数が減少に転じました。当コラムが出す必要のなかった緊急事態宣言として批判しているのはそれが理由です。

統計の初歩を理解しない専門家たち

最近、あるテレビの夕方のニュース番組で、よくテレビに出演するある大学の医学部の感染症の専門家がキャスターに「30代40代の人たちの感染とワクチン接種の関係はどうすれば解明できるか。」を問われて、「年単位のデータが集まってくれば、ひょっとすると年代別のワクチン接種と感染の関係が解明できるかもしれません。」と答えていました。

この人は多分統計学を学んだことがないのでしょうが、感染症や公衆衛生学の専門家が統計学を学んだことがないというのは柔道の選手が受け身の練習をしたことがないと言うくらい不思議なことのように思えます。

統計学には大雑把に言うと三種類あります。

一般に表やグラフを作ったり、平均や傾向を調べて状況を理解するというのが記述統計学であり、高校で学習します。

当コラムでの議論では母集団から一部のデータ（標本）を抜き出して、そのデータの特徴から母集団の特性を推測するという方法を取ることが多く、これは推測統計と呼びます。

推測統計では推定または検定という作業を行います。

推定では平均値など具体的な値を予測をし、検定では母集団について立てた仮説が正しいかどうかを統計学的に判定します。

さらに便利な手法としてベイズ統計があります。これは18世紀にベイズによって発見され、ラプラスによって確立されたベイズの定理を用いた統計学です。

統計学の教科書を書いているわけではないので細部には触れませんが、ベイズ統計では標本を必要とせずに様々な事象の性格を見極めることができます。

統計学的に説明すると

例えば、このベイズ統計をコロナ禍におけるPCR検査に応用してみます。

例えば、国民全体の1％がすでに新型コロナウイルスに感染していると仮定します。

さらにPCR検査方法では、実際に病気に罹患している人が陽性と判定される確率が95%、逆に罹患していない人が陰性と判定される確率は80%であると仮定します。

現在のPCR検査は大多数が医師が検査の必要があると認めた人が受けていますが、某テレビのコメンテーターが狂ったように主張している国民すべてが検査を受けるとして、ある人がこの検査を受けて陽性という判定を受けた時、本当にこのウイルスに感染している確率を計算してみます。

検査で陽性になる事象を事象A、検査で陰性になる事象を事象Ac、実際に感染している事象を事象B1、感染していない事象を事象B２とすると、求める確率はP（B1|A)となります。

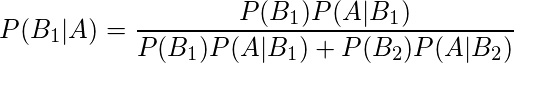
それぞれの確率は次のようになります。

• 病気に罹患している確率：P(B1)＝0.01
• 病気に罹患していない確率：P(B2)＝1-0.01＝0.99
• 実際に罹患している人が検査で陽性となる確率：P（A｜B1)＝0.95
• 実際に罹患していない人が検査で陰性となる確率：P（A｜B1)＝0.80
• 実際に罹患していない人が検査で陽性となる確率：P（A｜B2）＝１-0.8＝0.2
• これらの値を①の式に当てはめると、陽性と判定されたときに実際に感染している確率は4.75％であることが分かります。

当コラムが昨年の早い時期からPCR検査をむやみにやっても意味がなく、事態を混乱させるだけであると主張し続けたのはこのような計算が基礎にあります。100人が陽性と判定されても本当に陽性なのは5人しかいないということですからね。

皆さんの多くが癌検診を受けて、ポリープを採取するということがあっても実際に癌を宣告されることがほとんどないのと一緒です。

医師が必要と判断する場合にのみPCR検査をすればこの確率はかなり高くなりますので、意味がないということでもありませんが、このような理屈を理解しないテレビのコメンテーターなどに煽られると国策を誤ることになります。許されないのは感染症の専門家と称してテレビでコメントする医師や学者たちで、感染症学においては統計学は勉強しないのかと不思議に思うほどです。

ちなみにこの程度の計算は、経済学部で統計学の授業を選択した学生なら、最初の1年で学んでいます。

これを要するに

当コラムは危機管理の専門コラムであって医学的知識を持って執筆しているわけではありません。医学は当コラムの専門を遥かに超える領域です。しかし、社会現象となってデータが集まっていれば多くのことを理解することができます。

逆に医学的知識を持っていてもデータの扱いかたを知らない専門家たちは、目の前の患者を診ることは出来ても、社会全体で何が起きているのかを理解することができません。この度のコロナ禍で分かったことは、感染症の専門家というのは玉石混交であり、テレビにはディレクターの注文に応じるコメントをすることを意に介さない専門家ばかりが出てくるということです。