疑似相関

統計的証明とは

このコラムが危機管理の専門コラムであり、筆者が組織論、特に意思決定論を専門としていたことから、専門外の事象について観察する際には、自分の持っている知識・経験及び方法論が生かせる手法を駆使しています。

昨年冒頭から始まった新型コロナウイルスによる騒ぎを観察するに際し、当コラムが取った態度は、数理社会学の手法により観察された事象を意思決定論の立場から考察するというものでした。

この事態を理解するために医学関係の方々にいろいろと教えて頂いてはきましたが、そこから得た知見については伝聞の形をとって表現しています。

しかし、この医学的な知識経験を欠いていたことが却って役に立つこともありました。

多分、弊社に医学的知識や経験があったとすれば、そこに引っ張られて客観的に見ることが出来なかったかもしれない事象を、弊社の数理社会学的手法のみをもって理解しようとしたため、客観的かつ冷静に観たかもしれないという事象がいくつかあります。

当コラムでは共同通信が配信した東大の研究者チームがGoToトラベルに参加した人はしなかった人に比べて２倍の感染リスクがあることが統計学的に証明したとする記事をメディアが鵜呑みにしてGoToトラベル事業を批判したことを取り上げています。（専門コラム「指揮官の決断」 第231回　コロナ禍を危機にした人々：専門家たちの果たした役割　https://aegis-cms.co.jp/2301　）

この研究者チームの論文はエール大学の健康科学に関する査読前の論文がアップされているサイトで読むことが出来たのですが、統計学の入門的な講義を受けた者であれば即座に統計学的な証明ではないことが分かる論文です。英語を読む必要すらなく、記載されている式を見ただけで統計学的な証明になっていないことは一目瞭然です。書いた研究者たちはそれを熟知しており、彼ら自身が「統計学的な証明」と言っていないのです。

テレビに出てくる感染症の専門家たちは、この論文自体を読まずに共同通信の記事だけでコメントをしていましたし、多分、日本医師会会長も読まなかったのだと思います。筆者の知る限り、あれが統計学的証明とは言えないと言い切ったのは、ご自身もGoToトラベル事業の継続に反対していた尾身会長だけです。

それでは統計学的証明と言うためには何が必要なのでしょうか。

数学的にはいろいろな条件があるのですが、簡単に言うと相関関係と因果関係が明確にされていることが必要です。

例えばAという事象とBという事象があって、Aの変化に応じて規則的にBも変化していくことが観察されると、AとBの間には相関関係があると言われます。問題は、その相関関係に因果関係が認められるかどうかということなので、統計学的証明と言われるためには相関関係だけでなく、因果関係の存在も立証しなければなりません。

なぜなら相関関係が観察されても、因果関係がないことが多々あるからです。

例えば、火災現場へ出動する消防車の数と火災の規模の関係を見てみます。

火災が大規模であると出動する消防車の数は多くなります。しかし、消防車を多数出動させると火災が大きくなるということではありません。因果関係が逆転しています。

そのような事例は因果関係の誤謬と呼ばれます。

相関関係とは単純ではない

相関関係についても気を付けねばならないのは、一見して相関関係があるように見えて実はほとんど無関係であることもあることです。

よく例に出されるのは米国における調査で、アイスキャンディの売り上げと水難事故数の関係です。この二つのデーターはほとんど相似形を描くと言われています。つまり、相関関係だけを分析すると正の相関があると言うことができるのですが、因果関係があるとは言えません。

この二つの変数を考える時には、気温という第三の変数を考慮に入れる必要があります。そのような第三の変数は潜伏変数と呼ばれますが、どこに隠れているかを見抜かなければ事態の本質は読めないのです。

このように一見すると相関関係があるように見えるものを疑似相関と呼びますが、私たちは意外にこれに騙されることが多いようです。

何故なら、因果関係は相関関係だけでなく、専門的に言うと反事実的依存関係の存在が必要だからです。

たとえば、Aにある条件を与えた際にBという事態が生じたとします。反事実的依存関係とは、それではAにその条件を与えなかった場合にはどうなるのかという観察が必要なのですが、実験室的環境では可能であっても、実際の社会では時間を巻き戻すことが出来ないためにその依存関係の立証が難しいからです。

たとえば、正月に神社で賽銭を500玉で入れた場合と1000円札で入れた場合、その一年がどう変わるかなどは分からないのです。

統計学を全く理解しない感染症専門家が多数

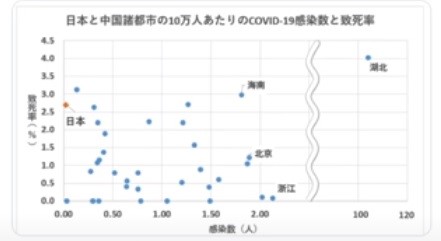
このグラフは特定非営利活動法人医療ガバナンス研究所の上昌広理事長が昨年ツイッターでツイートされた時に使用されたものですが、このツイッターで上氏は武漢と海南を除くと逆相関で、患者が多いところほど致死率が低いとしています。そして、どこまで軽い患者を診察しているかで致死率が決まることを意味しているとのコメントを付けられているのですが、これは疑似相関どころか、どこからどう見ても相関関係がない無相関の典型的な例です。

この人はどう考えても統計学の入門的知識すらお持ちでないのですが、テレビで解説をしている感染症専門家と言われる人たちの多くも同様です。致死率の計算すらまともにできないんですから。

本当によく分からないこともあります

このような間違いはすぐに分かるのですが、なかなか判断しにくい事例も多々あります。

たとえば、失業率と自殺者数のグラフはまったく相似形を描くことが知られており、相関関係を見出すことが出来そうですが、因果関係を簡単に見極めるわけにはいきません。自殺に至る原因は人それぞれですから、職を失ったことで自殺者が増えると簡単に断ずることもできないのです。自殺者数を扱うため、実験をすることもできず、研究室的環境での再現もできません。これが社会科学の不自由さでもあります。

しかし当コラムはあきらめることなく、持てる知識・経験・手法を駆使して、社会科学の方法論に忠実に事態の見極めをしてまいります。

当コラムのバックグラント異なるバックグランドをお持ちの方にも理解しやすいよう、入門的な解説を心掛けて参りますので、社会科学の初学者の方々の勉強になるようなコラムを作り上げていく所存です。